CAPITULO # 1
DIFERENCIAL E INTEGRAL DEFINIDA
1. Diferencial de una función
Veamos la figura:
2. Modelos basados en la diferencial y análisis de errores
Es muy útil la utilización de la diferencial para estimar los errores cometidos en aluna medición en especial. Es normal que a nuestro alrededor sea necesario determinar mediciones físicas, en las que se debe de considerar un valor exacto, que es el valor que se quiere medir o calcular. Pero en ocasiones también se presentan márgenes de error en dichas medidas, por lo que se debe de considerar de igual manera un valor aproximado.
La diferencial también nos sirve para realizar el cálculo de errores absolutos y las aproximaciones de los mismos.
Este procedimiento se puede realizar tal y como se muestra a continuación:
Si la función y=f(x) representa una medida física, su diferencial dy=df(x) es una aproximación del error absoluto de dicha medida.
Hablando de la aproximación del error absoluto, se necesita definir si dicho cálculo es aceptable o no, para eso se compara el resultado con el valor exacto, tal y como se indica a continuación. A dicho cálculo se le conoce como error relativo.
3. La notación suma.
La sumatoria o sumatorio (llamada también notación sigma ) es una operación matemática que se emplea para calcular la suma de muchos o infinitos sumandos.
La operación sumatoria se expresa con la letra griega sigma mayúscula Σ, y se representa así:
Expresión que se lee: " Sumatoria de Xi, donde i toma los valores desde 1 hasta n ".
i es el valor inicial, llamado límite inferior.
n es el valor final, llamado límite superior.
Pero necesariamente debe cumplirse que:
i ≤ n
Si la sumatoria abarca la totalidad de los valores, entonces no se anotan sus límites y su expresión se puede simplificar:
Si se quiere expresar la suma de los cinco primeros números naturales se puede hacer de esta forma:
EJEMPLO:
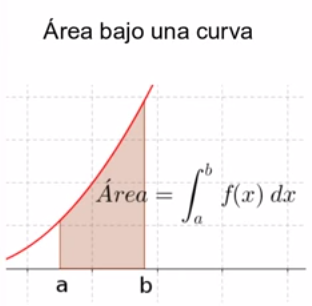
4. Área bajo la curva.
La interpretación geométrica de la regla de Barrow nos dice que la integral definida representa el área entre la curva y el eje de abcisas.
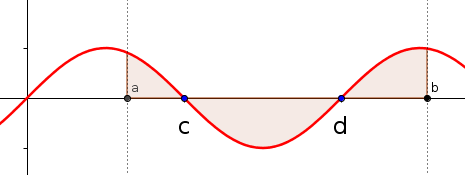
Si hacemos la integral definida entre a y b nos conduciría a un resultado erróneo. Habría que descomponer la integral en tres partes correspondientes a los intervalos [a,c] [c,d] y [d,b] y además tener en cuenta que en el intervalo [c,d] debemos tomar valor absoluto (porque saldría un área negativa al estar por debajo del eje).
Lo más práctico es tomar valor absoluto en todos los intervalos (y así no necesitamos saber los que están por encima y los que están por debajo). El área (A) de la imagen anterior se calcularía así:
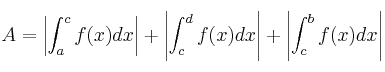
5. La integral definida y sus propiedades.
La integral definida de una función representa el área limitada por la gráfica de la función, en un sistema de coordenadas cartesianas con signo positivo cuando la función toma valores positivos y signo negativo cuando toma valores negativos.
Se simboliza de la siguiente manera:
- La integral definida se representa por
 .
.  es el signo de integración.
es el signo de integración.- a es el límite inferior de la integración.
- b es el límite superior de la integración.
 es el integrando o función a integrar.
es el integrando o función a integrar. es diferencial de
es diferencial de  , e indica cuál es la variable de la función que se integra.
, e indica cuál es la variable de la función que se integra.
Propiedades de la integral definida
1 El valor de la integral definida cambia de signo si se permutan los límites de integración.

2 Si los límites que integración coinciden, la integral definida vale cero.
![]()
3 Si ![]() es un punto interior del intervalo
es un punto interior del intervalo ![]() , la integral definida se descompone como una suma de dos integrales extendidas a los intervalos
, la integral definida se descompone como una suma de dos integrales extendidas a los intervalos ![]() y
y ![]() .
.

4 La integral definida de una suma de funciones es igual a la suma de integrales·
![Rendered by QuickLaTeX.com \displaystyle \int_{a}^{b}\left [ f(x)+g(x) \right ]\, dx=\int_{a}^{b}f(x)\, dx+\int_{a}^{b}g(x)\, dx](https://www.superprof.es/apuntes/wp-content/ql-cache/quicklatex.com-79107e587664d39f62804747b79bcc34_l3.png)
5 La integral del producto de una constante por una función es igual a la constante por la integral de la función.

6.Teorema de la media o del valor medio para integrales.
Si una función es continua en un intervalo cerrado ![]() , existe un punto
, existe un punto ![]() en el interior del intervalo tal que:
en el interior del intervalo tal que:


7. Teorema fundamental del cálculo.
El Teorema Fundamental del Cálculo proporciona un método abreviado para calcular integrales definidas, sin necesidad de tener que calcular los límites de las sumas de Riemann.
Conceptualmente, dicho teorema unifica los estudios de la derivación e integración, mostrando que ambos procesos son mutuamente inversos.
Teorema fundamental del cálculo:
Sea f una función integrable en el intervalo [a, b], entonces:
a) F es continua en [a, b]
b) En todo punto c de [a, b] en el que f sea continua se verifica que F es derivable en dicho punto, y F'(c) = f(c).
El Teorema Fundamental del Cálculo Integral nos muestra que F(x) es precisamente el área limitada por la gráfica de una función continua f(x).
A cada punto c en [a, b] se le hace corresponder el área Tc. Si calculamos la derivada de esa función:
Luego F'(c) = f(c), para todo c en [a, b]
Aparentemente, diferenciación e integración son dos procesos completamente diferentes. La diferenciación corresponde a un proceso de obtención de la tangente a una curva en un punto (o también el cambio en la velocidad), mientras que la integración corresponde a un proceso encaminado a encontrar el área bajo una curva. El Teorema Fundamental afirma que ambos procesos son inversos el uno del otro.
8. Método de sustitución.
El método de integración por sustitución o cambio de variable se basa en la derivada de la función compuesta.
![]()
10. Integrales que incluyen potencias de seno y coseno.
- La potencia del seno es impar y positiva. En este caso conservamos un factor seno y se pasan los restantes factores a coseno:
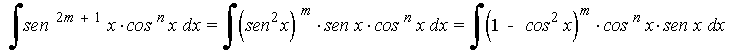





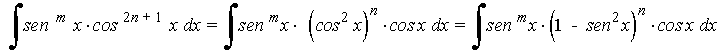
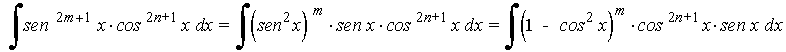
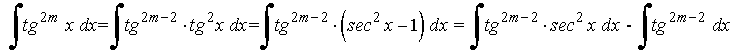
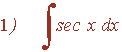


No hay comentarios.:
Publicar un comentario